【第2回】Python Marketing Data Analytics! ~データ確認の第一歩、可視化~
さて、前回に引き続き、銀行のキャンペーンマーケティングデータに基づく分析をネタにした勉強記録ですー。
データの可視化
まずは、データのheadを確認。
df.head()
| age | job | marital | education | default | balance | housing | loan | contact | day | month | duration | campaign | pdays | previous | poutcome | y | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 30 | unemployed | married | primary | no | 1787 | no | no | cellular | 19 | oct | 79 | 1 | -1 | 0 | unknown | no |
| 1 | 33 | services | married | secondary | no | 4789 | yes | yes | cellular | 11 | may | 220 | 1 | 339 | 4 | failure | no |
| 2 | 35 | management | single | tertiary | no | 1350 | yes | no | cellular | 16 | apr | 185 | 1 | 330 | 1 | failure | no |
| 3 | 30 | management | married | tertiary | no | 1476 | yes | yes | unknown | 3 | jun | 199 | 4 | -1 | 0 | unknown | no |
| 4 | 59 | blue-collar | married | secondary | no | 0 | yes | no | unknown | 5 | may | 226 | 1 | -1 | 0 | unknown | no |
実際にデータの内容を把握するため、グラフとして可視化してみることからスタートする。
まずは、分析したい対象に着目することがデータ分析の第一歩となる。
今回は、「y(定期預金の契約有無)」が対象だ。
このデータがどのような特性があるのか、このデータに影響を与えている変数はあるのか、
などを仮説を立てながら可視化し、検証していく。
sns.countplot(x='y', data=df)

データの大部分はnoの結果であることが分かる。
具体的な数値は集計時に確認してみる。
yesとnoの結果の違いは何からもたらされるのだろうか?
例えば、前回キャンペーンの効果結果は、今回のキャンペーンの結果による定期預金申込有無に効果を示しそうである。
sns.countplot(x='poutcome', hue='y', data=df)

データをみると、確かに前回結果がsuccessの群は、目的変数がyesとなっている人が多いことが分かる。
ただ、カテゴリごとのデータのサイズが大きく異なるため、単純なcountplotだけだと見にくいようだ。
これは、集計により比率等を算出してクロス集計を行ったり、
目的変数をダミー変数化して、数値データとして扱うことで、傾向を分かりやすく表現するなどの工夫が必要そうである。
カテゴリーデータ毎の可視化は、何らかの集計や加工をして可視化したほうが良さそうだ。
特に目的変数(今回でいえばy)が2値データの場合、ロジット関数をリンク関数としたモデル、
いわゆるロジスティック回帰モデルでモデリングしてみることが発生すると思われるので、ダミー変数化はほぼ必須である。
ダミー変数化とそれに伴う可視化・モデリング等はまた別の回で取り組んでみたい。
次に、数値データとカテゴリーデータの可視化はどうだろう?
まず気になるのは、ageとyの関係である。
age(年齢)は様々なデータ分析の説明変数になりやすい重要な要素である。
ageの分布をヒストグラムで可視化してみる。
plt.figure(figsize=(5,5)) plt.hist(df.age, bins=30) plt.show()

30歳代~40歳代が最もデータ数が多いようである。
60歳代以降になると人数は急激に減少する。
では次に、ageとyとの関係を確認しよう。
yの結果ごとにみた場合、ageの分布の傾向に特性がみられるかが焦点になる。
以下のとおりグラフを重ねて表示してみる。
age_y = df[df['y'] == 'yes']['age'] age_n = df[df['y'] == 'no']['age'] plt.figure(figsize=(5,5)) plt.hist(age_y, bins=30, alpha=0.5, color='cornflowerblue', label='$y=yes$') plt.hist(age_n, bins=30, alpha=0.5, color='mediumseagreen', label='$y=no$') plt.legend() plt.show()

y = no のサイズが大きいため、ヒストグラム自体を重ねると、分布の違いは比較できないようだ。 そこで、グラフを2つに分けて比較してみる。
fig, gr = plt.subplots(1,2,figsize=(12,5)) gr[0].hist(age_y, bins=30, color='cornflowerblue') gr[0].set_title('$y=yes$') gr[0].set_xlabel=('age') gr[1].hist(age_n, bins=30, color='mediumseagreen') gr[1].set_title('$y=no$') gr[1].set_xlabel=('age') plt.show()

y = yes の群のほうが、やや高齢層の比率が高いように思える。
年齢が高いほど yes の可能性が高くなるかどうかは、今後の検討材料になりそうだ。
データの分布は、もう少し分かりやすく描写する方法もある。
plt.figure(figsize=(8,5)) sns.distplot(df['age'], bins=30, color='cornflowerblue') plt.show()

上記のグラフは、カーネル密度推定を行ったグラフである。
データから推定した確率密度関数を描写しており、データの背後にあると想定される確率分布が可視化できる。
カーネル密度推定については、以下wikiを参照するとよい。
カーネル密度推定
これを使えば、異なるカテゴリの分布の違いが比較的分かりやすく描写できる。
fig = sns.FacetGrid(df, hue='y', aspect=4) fig.map(sns.kdeplot, 'age', shade=True) fig.add_legend() plt.show()

上記のとおり、yes、noの群では、若年層と高齢層で差がみられる。
yesの群のほうが分散が大きいようである。
各変数間のデータの状況を知りたいときは、sns.pairplotを利用すると便利だ。
データフレームの数値データだけになるが、それぞれの散布図行列図を出力できる。
回帰直線も描写されるため、相関関係も(なんとなく)把握できる。
sns.pairplot(df, hue="y", size=2, kind='reg', diag_kind='kde') plt.show()
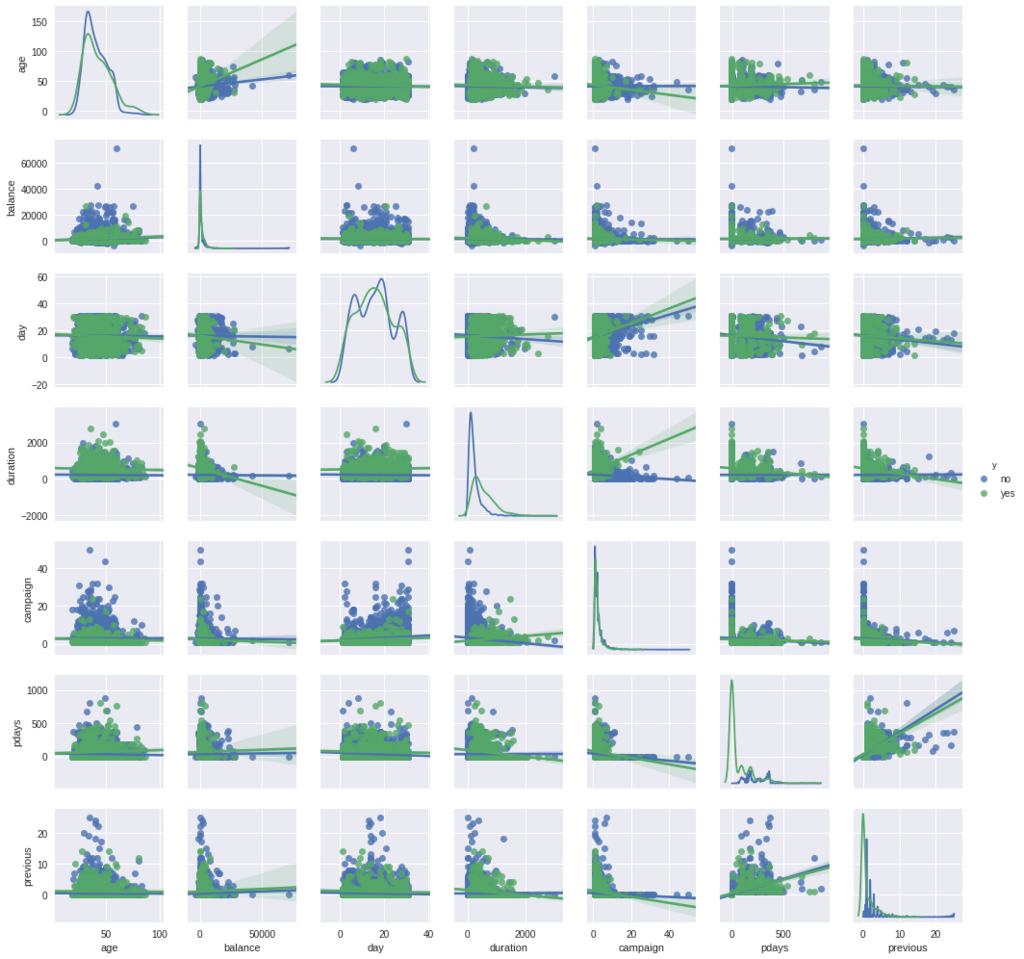
グラフだけみると、balanceとageの関係について、y = yesの群では正の相関がありそうな描写となっている。
これを確かめるため、この変数だけにしぼって描写してみる。
sns.jointplot('balance','age', df[df['y']=='yes'], kind="reg") plt.show()

このデータをみると、ageとbalanceの間に相関関係はほとんどみられないことが分かる。
単に見た目の問題ではなく、きちんと数値で確認することが重要なようだ。
データセットを構成する変数同士の相関(連関)が、後々回帰分析を行う際のマルチコ(多重共線性)の有無を把握する際に重要になることがある。
変数同士の相関については、相関行列図を描写することが最も相関関係が分かりやすいため、どこかで実施していくことが必須になる。
なお、相関=因果ではないことは特に気を付けて分析してくべきだ。 疑似相関の問題も常に念頭に入れておくと良いと思う。
次に、前回に少し着目したbalanceの分布についてもう少し詳細に確認してみることにする。
まずはKDEプロットを行う。
fig = sns.FacetGrid(df, hue='y', aspect=5) fig.map(sns.kdeplot, 'balance', shade=True) fig.add_legend() plt.show()

記述統計の際に推察したとおり、右裾がとても長い分布になっているようである。
分布の形状に関しては、ヴァイオリンプロットと呼ばれるグラフも分かりやすい。
sns.factorplot(x='y', y='balance', data=df, kind='violin',aspect=2) plt.show()

balanceは裾が長い分布であるのでかなり分かりづらいかもしれないが、
ageを例にもう一度描写してみると、分布についてよく分かる。
sns.factorplot(x='y', y='age', data=df, kind='violin',aspect=2) plt.show()

バイオリンプロットは、3変数の分布も大変分かりやすく描写してくれる。
以下は、「婚姻状況(marital)」、「年齢(age)」、「定期預金契約(y)」の分布。
ax = sns.violinplot(x="marital", y="age", hue="y",aspect=.5, data=df, split=True) plt.show()

単身者は低年齢、婚姻・離婚者は中央値はやはり高く、分散も大きい。
また、高齢の定期預金契約者が多いのはmarriedとdivorcedが顕著である。
今後の解析において、データが正規分布に基づいているか確認することが必要になるケースがある。
balanceとageの正規性を確認してみたい。
plt.figure(figsize=(5,5)) gr = stats.probplot(df['age'], plot=plt) plt.title('age') plt.show()

plt.figure(figsize=(5,5)) gr = stats.probplot(df['balance'], plot=plt) plt.title('balance') plt.show()

上記グラフはQ-Qプロットと呼ばれる。
観測値がある確率分布に従う場合の期待値と観測値のデータを2次元に表示したものだ。
今回は正規分布を理論分布と仮定しているため、正規Q-Qプロットなどと呼ばれる。
データの青いプロットが、赤いラインに沿えばこのデータが正規分布に従っていると判断できる。
しかし、age,balanceのいずれも両側が上向きに歪んでおり、正規分布以上に裾が広がっていると考えられる。
正規性を仮定した分析は好ましくないようだ。
直観的な解釈ではなく、客観的に検定を行う手法もある。
Shapiro-Wilk検定やKolmogorov-Smirnov検定がそれにあたる。
ただし、昨今はビッグデータとよばれる大量データを分析することが多いようであるため、検定を行うシチュエーションは減っているようである。
(サンプルサイズが大きいほど、p値が小さくなるため)
stats.shapiro(df['age'])
(0.9595122933387756, 9.410944406190885e-34)
stats.shapiro(df['balance'])
(0.5015109777450562, 0.0)
いずれもp値は0.05を下回るため、帰無仮説(データは正規分布に従う)は棄却される。
つまり、両データとも正規性を有しないデータであることが分かる。
ただし、本データはサイズが大きく、P値が優位になりやすいため、検定は適切ではなさそうではあるが、
ひとつのテクニックとして覚えておくと良さそうだ。
終わりに
ここまで書いた後でしたが、欠損値補完を完全に飛ばしてたー。
まぁ、どこかの段階でやりましょう。
Pythonだと限界があるので、Rを呼び出してみる必要性があるかも。
とりあえず、このまま進めちゃえってことで、次はクロス集計と検定をやりまーす。