Python機械学習タスクにおける欠損補完の精度をいろいろ検証してみた件。
社内機械学習コンペにて、欠損補完の精度およびシミュレーションが個人的課題になったので、
振り返りの自習&覚書です。
※この記事の欠損処理方法は、理論的に正しくない・妥当でない場合が多々あるかもしれません。 中の人の勉強不足なので、さらっと流していただくか、正しい認識をご教示いただけると喜びます。 処理内容間違ってたらぜひお知らせくださいm(__)m
※なお、本記事は以下Colaboratory公開ノートブックの焼き直しです。
今回の自習内容は、sklearn や fancyimpute 等、欠損値・行列補完アルゴリズムによる欠損値補完処理により、機械学習による推計精度にどの程度影響するか、様々なパターンをシミュレーションすることで、今後の機械学習タスクの参考にしようとするものです。
まずは必要なライブラリ準備。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import fancyimpute from sklearn.datasets import load_boston import warnings warnings.filterwarnings('ignore') # 実行に影響ないアラートを無視 np.random.seed(123)
統計科学では、欠損値は主に以下3分類で考えられるケースが多いです。
| 欠損値の種類 | 内容 |
|---|---|
| MCAR (Missing Completely At Random) | 完全にランダムに欠損 |
| MAR (Missing At Random) | 観測データに依存する欠損 |
| MNAR (Missing Not At Random) | 欠損データに依存する欠損 |
完全にランダムな欠損(MCAR)
データに依存せずに発生する欠損値です。
観測データに依存する欠損(MAR)
欠損有無が、他のデータと相関する欠損値です。
(例えば、男性は欠損値が多い、夜の時間は欠損値が多い etc)
欠損データに依存する欠損(MNAR)
欠損有無が、欠損データそのものと相関している欠損値です。データを見ただけでは判別が難しいのが特徴です。
(例えば、データが大きいほど欠損値の確率が増える etc)
参考:Suny side up!:欠損値があるデータの分析(清水裕士)
この記事では上記3種の欠損を意図的に発生させ、
各種欠損値処理の方法により、 target をどの程度正確に予測できるかを検証します。
1 sklearn Boston データセット
今回利用するデータセットはsklearnのサンプルデータbostonデータセットです。
boston = load_boston() target = pd.DataFrame(boston.target) boston_df = pd.DataFrame(boston.data, columns=boston.feature_names) target.columns = ["target"] boston_df = pd.concat([boston_df, target],axis=1) print("bostonデータセット:",boston_df.shape) display(boston_df.head(3))
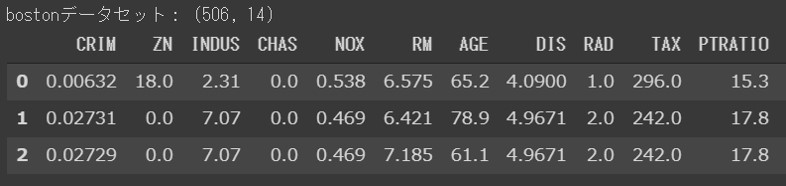
1-1 欠損値データセットの作成
bostonデータセット全体の506レコード中、任意の100レコードについて、欠損値生成を行った3種のデータを用意します。
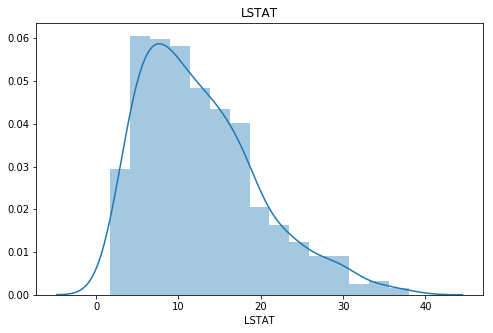
欠損を発生させるカラムは LSTATです。( 給与の低い職業に従事する人口の割合 (%))
これは比較的 target と相関が高く、データが適度に散布されているため、このカラムを選定しています。
plt.figure(figsize=(8,5),facecolor="white") sns.distplot(boston_df["LSTAT"]) plt.title("LSTAT") plt.show() sns.relplot(data=boston_df, x="LSTAT", y="target",height=5,aspect=1.5) plt.title("LSTAT * target") plt.show()

MCAR
完全無作為に欠損値を生成したDataFrameを boston_df_mcar として格納します。
np.random.seed(123) rand_mcar = np.sort(np.random.choice(boston_df.index,100,replace=False)) def make_null(df,index,col_name): # 欠損値代入の関数です。以下、この関数を流用します。 df1 = df.drop(index) df2 = df.iloc[index, :] df_c = df2[col_name] df2[col_name] = np.nan result_df = pd.concat([df1,df2]).sort_index() return result_df, df_c boston_df_mcar , mcar_correct = make_null(boston_df, rand_mcar, "LSTAT")
MAR
その他観測地と相関のある欠損生成を行います。
少し簡易的ですが、カラム AGE の上位200レコードから80レコード、下位200レコードから20レコード分の欠損値を無作為に生成します。
top200 = boston_df.sort_values("AGE",ascending=False).head(200) under200 = boston_df.sort_values("AGE",ascending=True).head(200) rand_top = np.random.choice(top200.index,80,replace=False) rand_under = np.random.choice(under200.index,20,replace=False) rand_mar = np.hstack((rand_top, rand_under)) boston_df_mar , mar_correct = make_null(boston_df, rand_mar, "LSTAT")
MNAR
欠損データそのものに依存した欠損生成を行います。
ここでは極端ですが、
カラム LSTAT の上位100レコードを欠損値にします。
np.random.seed(789) top_mnar100 = boston_df.sort_values("LSTAT",ascending=False).head(100) rand_mnar = np.random.choice(top_mnar100.index,100,replace=False) boston_df_mnar , mnar_correct = make_null(boston_df, rand_mnar, "LSTAT")
1-2 欠損データの形状確認
これで、3種の欠損パターンを生成したデータセットが完成しました。 内容を少し確認します。
print("3つのデータセットの形状確認") print(boston_df_mcar.shape) print(boston_df_mar.shape) print(boston_df_mnar.shape) print("欠損処理した「LSTAT」カラムのデータ確認") plt.figure(figsize=(10,4),facecolor="white") sns.distplot(boston_df["LSTAT"]) sns.distplot(boston_df_mcar.dropna()["LSTAT"]) sns.distplot(boston_df_mar.dropna()["LSTAT"]) sns.distplot(boston_df_mnar.dropna()["LSTAT"]) plt.legend(["master","MCAR","MAR","MNAR"]) plt.show()
3つのデータセットの形状確認
(506, 14)
(506, 14)
(506, 14)
欠損処理した「LSTAT」カラムのデータ確認
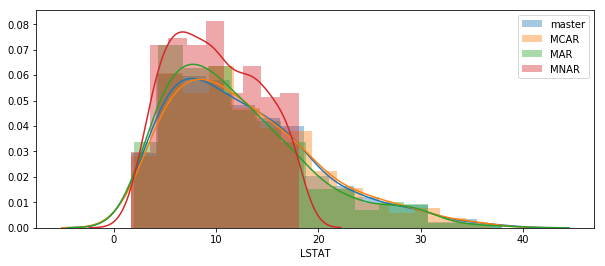
LSTATカラムは MCAR < MAR < MNAR の順にいびつな形状になっているようです。
1-3トレーニングデータと予測対象データの作成
学習させるデータと、予測するデータを分割します。
3つのデータセットがありますが、予測対象にするデータはそれぞれ同じインデックスとし、比較対象できるように設計します。
np.random.seed(999) rand_i = np.sort(np.random.choice(boston_df.index,100,replace=False)) mcar_train = boston_df_mcar.drop(rand_i) mcar_test = boston_df_mcar.iloc[rand_i,:] mar_train = boston_df_mar.drop(rand_i) mar_test = boston_df_mar.iloc[rand_i,:] mnar_train = boston_df_mnar.drop(rand_i) mnar_test = boston_df_mnar.iloc[rand_i,:]
作成したデータを以下のとおり整理します。
| データセット | 内容 |
|---|---|
| target | trainの予測用正解データ |
| answer | testの正解データ(精度検証用) |
| mcar_train | MCARによるデータセット(train) |
| mcar_test | MCARによるデータセット(test) |
| mar_train | MARによるデータセット(train) |
| mar_test | MARによるデータセット(test) |
| mnar_train | MNARによるデータセット(train) |
| mnar_test | MNARによるデータセット(test) |
2 欠損値補完
欠損値の補完方法には、いくつかの種類があります。
リストワイズ
1つでも欠損値のあるサンプル(または変数)は分析から除外 ※厳密にはサンプル削除はリストワイズとは呼ばないかもしれません。
ここでは便宜上、両者をリストワイズ(rowとcolumnで区分)と呼ばせていただきます。ペアワイズ
分析対象にする変数に欠損値が含まれていなければすべて分析対象に含める単一代入
欠損を何らかのデータで補完する多重代入 欠損値に異なる値を推定した複数のデータを生成し、その分析結果を統合し補完する
ペアワイズは機械学習に向いておらず、多重代入は簡易に実行するパッケージが整備されていません。
そこで、本のノートブックでは、リストワイズと単一代入をいくつかのパターンで組み合わせ、どのように精度が変化するか検証します。
2-1 trainデータの欠損処理
trainデータは、主に2種類の処理方法があります。
リストワイズで欠損値を含むcolumn、またはサンプル(row)を削除する
欠損値を補完する、または欠損値の情報を埋め込む
「1」のケースは、欠損データと比較してtrainデータの量が多く、欠損値の種類がMCARであることが自明なときに行うことが多いと思われます。
一部の欠損したサンプル(row)を削除しても、学習には支障がないと判断した場合、こちらの処理のほうが適切かもしれません。
(補完する処理は、一般的にはバイアスを生み、精度としては実データより悪くなることが想定されるためです)
ただし、以下のようなケースでリストワイズによりcolumn, rowを削除するのは適切だとは言えません。
- 欠損がMAR, MNARの(可能性がある)ケースでrowを削除する
欠損しているデータに何らかの傾向があるため、安易に欠損しているレコード(row)を削除すると、データセットに偏りが生じる可能性があります。
- 欠損が存在するcolumnが、targetの精度に強く影響するにも関わらずcolumnを削除する
欠損が生じているcolumnそのものを削除することも手法としてはありますが、targetの精度に影響するような重要なデータである場合、column丸ごと捨ててしまうのは適切であるとは言えません。
このケースでは、多少バイアスが発生したとしても、補完するなどの処理をしたほうが有効である場合が多々あります。
また、そもそもcolumnの数が少ない場合などは、なるべくデータを有効活用するよう、安易に削除しないほうが良いと思われます。
「2」のケースは、元々のデータ数が少ない場合や、欠損値がMAR, MNARの可能性が捨てきれない場合の対応がほとんどです。
単一代入方法については、今回は以下2種を試すこととします。
| 項目 | 内容 |
|---|---|
| 代表値代入法 | 平均値・中央値・最頻値など、欠損があるcolumnの統計表を代入する方法。 |
| (確率的)回帰代入法 | 欠損していない変数を説明変数として欠損値を予測する方法。 |
代表値代入法
簡易にデータ補完できる反面、データのバイアスがかなり大きくなることが懸念される手法です。回帰代入法
統計モデル(機械学習モデル)を使用し、欠損値を予測します。他のデータを使用して予測するため、比較的バイアスを抑えられることが予測される。
また、この中には分類されませんが、Pythonパッケージの fancyimputeには欠損補完用の行列補完アルゴリズムがいくつか用意されています。
今回はこのパッケージ内のアルゴリズムもいくつか選定し、試してみることにします。
2-2 testデータの欠損処理
testデータの欠損処理方法については、注意すべき点が2点あります。
リストワイズ(row)は不可
モデルを学習するためのtrainデータでは、どのデータを学習に用いるかは設計者が自由に調整できます。
この点から、欠損が発生しているサンプル(row)を削除することは問題ありません。
しかし予測対象のサンプル(row)を任意に削除することはできません。
「このサンプルは予測しません」ということは実務上でも競技上でも許されません。単一代入の平均値や学習データはtrainを使用
代入するデータに使用する統計量やモデルは、trainデータから学習させなければなりません。 ※ 予測対象データは、課題によって1レコードずつ与えらるデータかもしれません。 また、予測対象のデータを学習に使用すると、予測対象が違うたびにモデルも異なった内容になってしまい、実務上は好ましくありません。
したがって、代入に使用するデータはすべてtrainデータを基にすることが原則となっています。
2-2 欠損補完データの生成
上記踏まえ、3種のデータフレームにを基にした欠損処理後データフレームを作成します。
| 削除方法 | 内容 | 適用データ |
|---|---|---|
| A リストワイズ(row) | 欠損が発生しているレコード(row)の削除 | trainのみ |
| B 平均値代入 | trainデータの平均を代入 | train, test |
| C 回帰代入(LinearRegression) | 線形モデルによる推計値を代入 | train, test |
| D 回帰代入(RandomForest) | ランダムフォレストによる推計値を代入 | train, test |
| E 回帰代入(LightGB) | LightGBMによる推計値を代入 | train, test |
| F 行列補完(KNN) | fancyimpute.KNN(最近傍法)を利用した行列補完 | train, test |
| G 行列補完(softimpute) | fancyimpute.softimpute(SVD分解の反復処理)を利用した行列補完 | train, test |
まず、train,testデータセットのリストを作成し、同リストを引数として渡すと、代入したリストを返す関数を作成していきます。
mcar_list = [mcar_train, mcar_test] mar_list = [mar_train, mar_test] mnar_list = [mnar_train, mnar_test]
A リストワイズ(row)
欠損が発生しているレコード(row)を削除します。
def listwise_row(df_list): for i,df in enumerate(df_list): if i == 0 : result_df = df.dropna() else: pass return result_df mcar_A_train = listwise_row(mcar_list) mar_A_train = listwise_row(mar_list) mnar_A_train = listwise_row(mnar_list)
B 平均値代入
欠損値に平均値を代入します。
def sub_mean(df_list): df1 = df_list[0].fillna(df_list[0].mean()) df2 = df_list[1].fillna(df_list[0].mean()) return df1, df2 mcar_B_train, mcar_B_test = sub_mean(mcar_list) mar_B_train, mar_B_test = sub_mean(mar_list) mnar_B_train, mnar_B_test = sub_mean(mnar_list)
C 回帰代入(LinearRegression)
scikit-learnのLinearRegressionを用いた回帰代入を行います。
from sklearn.linear_model import LinearRegression def sub_lr(df_list): train_master = df_list[0].dropna() train_miss = df_list[0][df_list[0].isnull().any(axis=1)] test_master = df_list[1].dropna() test_miss = df_list[1][df_list[1].isnull().any(axis=1)] model = LinearRegression().fit(train_master.drop(["LSTAT","target"],axis=1), train_master["LSTAT"]) train_miss["LSTAT"] = model.predict(train_miss.drop(["LSTAT","target"],axis=1)) test_miss["LSTAT"] = model.predict(test_miss.drop(["LSTAT","target"],axis=1)) train = pd.concat([train_master,train_miss]).sort_index() test = pd.concat([test_master,test_miss]).sort_index() return train, test mcar_C_train, mcar_C_test = sub_lr(mcar_list) mar_C_train, mar_C_test = sub_lr(mar_list) mnar_C_train, mnar_C_test = sub_lr(mnar_list)
D 回帰代入(RandomForest)
scikit-learnのRandomForestを用いた回帰代入を行います。
from sklearn.ensemble import RandomForestRegressor def sub_rfr(df_list): train_master = df_list[0].dropna() train_miss = df_list[0][df_list[0].isnull().any(axis=1)] test_master = df_list[1].dropna() test_miss = df_list[1][df_list[1].isnull().any(axis=1)] model = RandomForestRegressor(random_state=1).fit(train_master.drop(["LSTAT","target"],axis=1), train_master["LSTAT"]) train_miss["LSTAT"] = model.predict(train_miss.drop(["LSTAT","target"],axis=1)) test_miss["LSTAT"] = model.predict(test_miss.drop(["LSTAT","target"],axis=1)) train = pd.concat([train_master,train_miss]).sort_index() test = pd.concat([test_master,test_miss]).sort_index() return train, test mcar_D_train, mcar_D_test = sub_rfr(mcar_list) mar_D_train, mar_D_test = sub_rfr(mar_list) mnar_D_train, mnar_D_test = sub_rfr(mnar_list)
E 回帰代入(LightGBM)
lightgbmを用いた回帰代入を行います。
from lightgbm import LGBMRegressor from sklearn.model_selection import train_test_split def sub_lgbm(df_list): train_master = df_list[0].dropna() train_miss = df_list[0][df_list[0].isnull().any(axis=1)] test_master = df_list[1].dropna() test_miss = df_list[1][df_list[1].isnull().any(axis=1)] X_train, X_val, y_train, y_val = train_test_split(train_master.drop(["LSTAT","target"],axis=1), train_master["LSTAT"], test_size=0.2, random_state=1) model = LGBMRegressor(random_state=1).fit(X_train, y_train, eval_set=[(X_val, y_val)], eval_metric = "mean_squared_error", early_stopping_rounds=20, verbose=20) train_miss["LSTAT"] = model.predict(train_miss.drop(["LSTAT","target"],axis=1)) test_miss["LSTAT"] = model.predict(test_miss.drop(["LSTAT","target"],axis=1)) train = pd.concat([train_master,train_miss]).sort_index() test = pd.concat([test_master,test_miss]).sort_index() return train, test mcar_E_train, mcar_E_test = sub_lgbm(mcar_list) mar_E_train, mar_E_test = sub_lgbm(mar_list) mnar_E_train, mnar_E_test = sub_lgbm(mnar_list)
F 行列補完(KNN)
fancyimpute KNN による最近傍法を利用した行列補完
from fancyimpute import KNN def sub_knn(df_list): model = KNN(k=3) result_list=[] for i,df in enumerate(df_list): df_c = df.copy() pred = model.fit_transform(df_c.drop("target",axis=1)) df_c["LSTAT"] = pred[:,12] result_list.append(df_c) return result_list[0], result_list[1] mcar_F_train, mcar_F_test = sub_knn(mcar_list) mar_F_train, mar_F_test = sub_knn(mar_list) mnar_F_train, mnar_F_test = sub_knn(mnar_list)
G 行列補完 (softimpute)
fancyimpute softimputeによる行列補完
from fancyimpute import BiScaler, SoftImpute def sub_soft(df_list): norm = BiScaler() model = SoftImpute() result_list = [] for i, df in enumerate(df_list): df_c = df.copy() pred = model.fit_transform(df_c.drop("target",axis=1).values) df_c["LSTAT"] = pred[:,12] result_list.append(df_c) return result_list[0], result_list[1] mcar_G_train, mcar_G_test = sub_soft(mcar_list) mar_G_train, mar_G_test = sub_soft(mar_list) mnar_G_train, mnar_G_test = sub_soft(mnar_list)
2-3 train, test全パターンデータの整理
# train_list mcar_train_list = [mcar_A_train, mcar_B_train, mcar_C_train, mcar_D_train, mcar_E_train, mcar_F_train,mcar_G_train] mar_train_list = [mar_A_train, mar_B_train, mar_C_train, mar_D_train, mar_E_train, mar_F_train, mar_G_train] mnar_train_list = [mnar_A_train, mnar_B_train, mnar_C_train, mnar_D_train, mnar_E_train, mnar_F_train, mnar_G_train] # test_list mcar_test_list = [mcar_B_test, mcar_C_test, mcar_D_test, mcar_E_test, mcar_F_test, mcar_G_test] mar_test_list = [mar_B_test, mar_C_test, mar_D_test, mar_E_test, mar_F_test, mar_G_test] mnar_test_list = [mnar_B_test, mnar_C_test, mnar_D_test, mnar_E_test, mnar_F_test, mnar_G_test]
3 学習・予測・精度検証
この時点で、MCAR, MAR, MNARで作成した欠損を補完したデータフレームが、それぞれ補完方法の違いによりA~Hの種類で準備しました。
ここから、MCAR, MAR, MNARごとに学習・予測・精度検証を行い、どのような欠損にはどのような補完方法が適当なのかシミュレーションしていきます。
なお、精度検証で利用する機械学習アルゴリズムは線形モデル(LinearRegression)とツリーモデル(RandomForest)とします。
評価指標はMSE(平均二乗誤差)とし、MSEが少ないほうが精度が良いとされます。
3-1 精度検証用の予測モデルの作成と精度抽出
まず、以下のとおり使用ライブラリをインポートします。
from sklearn.linear_model import LinearRegression from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import mean_squared_error
線形モデル(LinearRegression)により、全train, testデータの組み合わせによるMSE精度をリスト化します。
# 線形モデルによる精度リストの抽出 lr = LinearRegression() def predict(train_list, test_list, model): mse_list = [] for i,train in enumerate(train_list): train_X = train.drop("target",axis=1) target = train["target"] model.fit(train_X,target) for j,test in enumerate(test_list): test_X = test.drop("target",axis=1) true = test["target"] pred = model.predict(test_X) metric = mean_squared_error(true, pred) mse_list.append(metric) return mse_list MCAR_LR = predict(mcar_train_list, mcar_test_list, lr) MAR_LR = predict(mar_train_list, mar_test_list, lr) MNAR_LR = predict(mnar_train_list, mnar_test_list, lr)
以下で、MCAR, MAR, MNARそれぞれのデータフレームに整えます。
MCAR_LR_df = pd.DataFrame(np.array(MCAR_LR).reshape(7,6)) MCAR_LR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MCAR_LR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"] MAR_LR_df = pd.DataFrame(np.array(MAR_LR).reshape(7,6)) MAR_LR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MAR_LR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"] MNAR_LR_df = pd.DataFrame(np.array(MNAR_LR).reshape(7,6)) MNAR_LR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MNAR_LR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"]
続いて、ツリーモデル(ランダムフォレスト)を使用して同様の手順を繰り返します。
rfr = RandomForestRegressor(random_state=1) def predict(train_list, test_list, model): mse_list = [] for i,train in enumerate(train_list): train_X = train.drop("target",axis=1) target = train["target"] model.fit(train_X,target) for j,test in enumerate(test_list): test_X = test.drop("target",axis=1) true = test["target"] pred = model.predict(test_X) metric = mean_squared_error(true, pred) mse_list.append(metric) return mse_list MCAR_RFR = predict(mcar_train_list, mcar_test_list, rfr) MAR_RFR = predict(mar_train_list, mar_test_list, rfr) MNAR_RFR = predict(mnar_train_list, mnar_test_list, rfr)
MCAR_RFR_df = pd.DataFrame(np.array(MCAR_RFR).reshape(7,6)) MCAR_RFR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MCAR_RFR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"] MAR_RFR_df = pd.DataFrame(np.array(MAR_RFR).reshape(7,6)) MAR_RFR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MAR_RFR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"] MNAR_RFR_df = pd.DataFrame(np.array(MNAR_RFR).reshape(7,6)) MNAR_RFR_df.columns = ["test_mean","test_LR","test_RFR","test_LGBM","test_KNN","test_soft"] MNAR_RFR_df.index = ["train_listwise","train_mean","train_LR","train_RFR","train_LGBM","train_KNN","train_soft"]
上記までの処理で、精度検証のデータがすべて整いました。
3-2 精度の可視化と評価
最後に、精度を可視化・分析するためのコードを記載していきます。
def bar_data(df1,df2): df_list=[df1, df2] result = pd.DataFrame() for i,df in enumerate(df_list): s_df = df.stack().reset_index() s_df.columns = ["b","c","mse"] if i == 0: s_df["a"] = "Model_LR : " else : s_df["a"] = "Model_RFR : " s_df["predict_model"] = s_df["a"]+":"+s_df["b"]+":"+s_df["c"] s_df = s_df[["predict_model","mse"]] result = pd.concat([result, s_df]).sort_values(by="mse") return result MCAR_result = bar_data(MCAR_LR_df,MCAR_RFR_df) MAR_result = bar_data(MAR_LR_df,MAR_RFR_df) MNAR_result = bar_data(MNAR_LR_df,MNAR_RFR_df)
def barplot(df,title): plt.figure(figsize=(5,30),facecolor="white") plt.title(title) sns.barplot(data = df, x="mse", y="predict_model") plt.show(); def heatmap(df,title): plt.figure(figsize=(10,7),facecolor="white") plt.title(title) sns.heatmap(df,annot=True,fmt="1.1f",cmap="coolwarm",) plt.show();
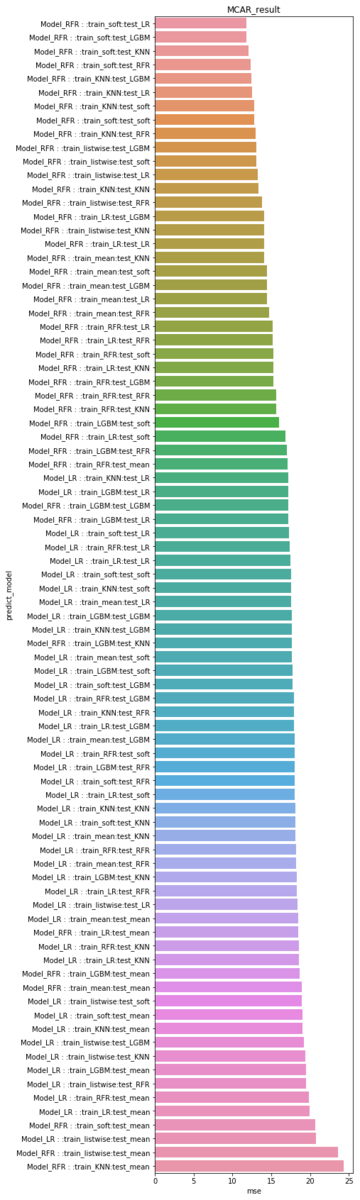
MCAR、MAR、MNARごとの精度ランキング
MCARの精度は、trainデータをsoftimputeで補完し、LRやLGBMなど、機械学習系のモデルでtestデータを補完したデータセットが精度上位にきています。
testデータをmeanで補完したモデルは総じて成績が悪く、安易に使用しないほうがよさそうです。
また、targetの予測モデルはLRよりもRFRが優秀です。
barplot(MCAR_result,"MCAR_result")
MARのデータセットではtrainデータをリストワイズ(row)で除去したモデルが優秀です。 欠損が別column(ここでは AGE )と相関しているため、無理に補完するよりも、その行そのものがtrainデータに混ざらない方が汎化性能が高まるようです。
こちらも testデータをmeanで置き換えるのは成績が悪く、最終のtarget予測モデルはRFRが高精度です。
barplot(MAR_result,"MAR_result")
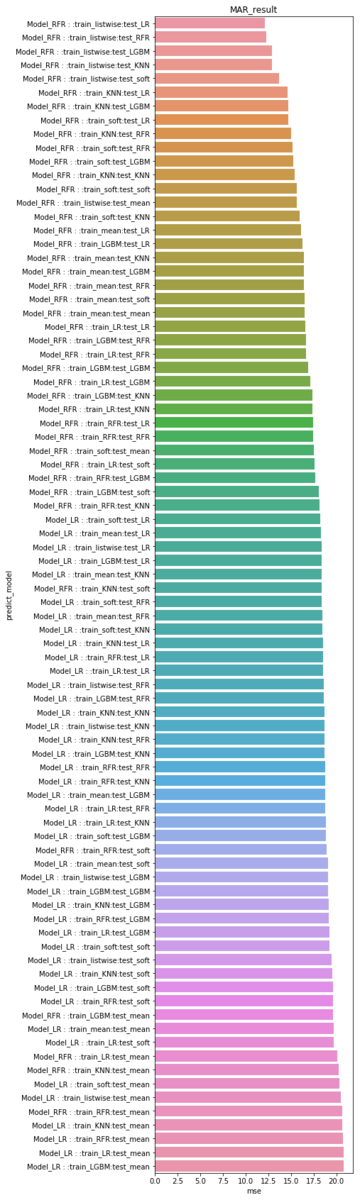
MNARは特徴的で、trainデータをmeanで置き換えるモデルが比較的上位にきています。 (統計学の世界では禁則に近いtrain, testともにmean置換が精度で3位!)
平均値置換でなぜ精度が上がるのか考察が深まっていませんが、様々はパターンで検証の余地がありそうです。
barplot(MNAR_result,"MNAR_result")

LR, RFRのヒートマップと精度差分
ここでは、精度のヒートマップを用いて傾向を可視化しています。
また、LRとRFRの精度を比較し、相対的にどちらのモデルのほうが精度が高いか可視化しています。
上段がLRで予測したモデルの精度、中断がRFRで予測したモデルの精度、下段が両モデルの差分となっています。
MCARでは、3段目がほとんど赤いヒートマップとなっているため、RFRのほうが各パターンにおける精度が高いようです。
LRではtestデータをLRで予測したモデルの精度が高い傾向です。
RFRではtrainデータをsoftimputeで予測したモデルの精度が高い傾向です。
heatmap(MCAR_LR_df,"MCAR_LR: heatmap") heatmap(MCAR_RFR_df,"MCAR_RFR: heatmap") heatmap(MCAR_LR_df - MCAR_RFR_df,"MCAR : LR - RFR : heatmap")


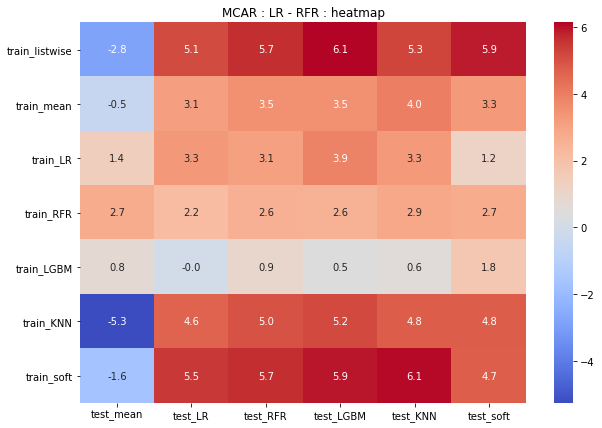
MARでは、RFRで予測したモデルのうち、trainをリストワイズ除去したモデルの精度がやはり高いことがわかります。
LRの予測モデルでは、train_meanやtrain_softが優秀です。
heatmap(MAR_LR_df,"MAR_LR: heatmap") heatmap(MAR_RFR_df,"MAR_RFR: heatmap") heatmap(MAR_LR_df - MAR_RFR_df,"MAR : LR - RFR : heatmap")


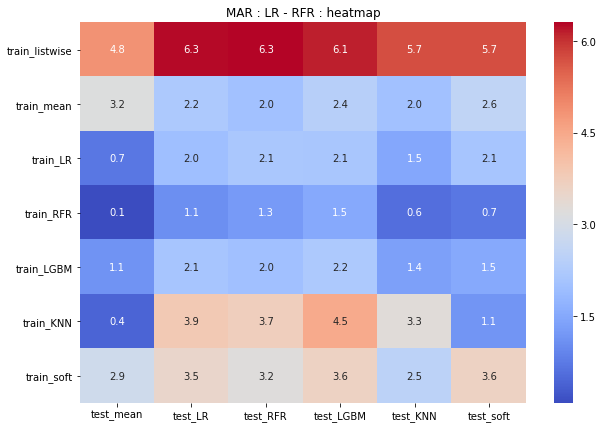
MNARは、LRモデルの予測値はどれも安定している一方、RFRは精度に大きなばらつきがあります。
バイアスにより、一部モデルでは過学習が起こっている可能性が推察できます。
ただし、testデータの補完方法によっては、かなり高い精度で推計できていることもわかります。
heatmap(MNAR_LR_df,"MNAR_LR: heatmap") heatmap(MNAR_RFR_df,"MNAR_RFR: heatmap") heatmap(MNAR_LR_df - MNAR_RFR_df,"MNAR : LR - RFR : heatmap")


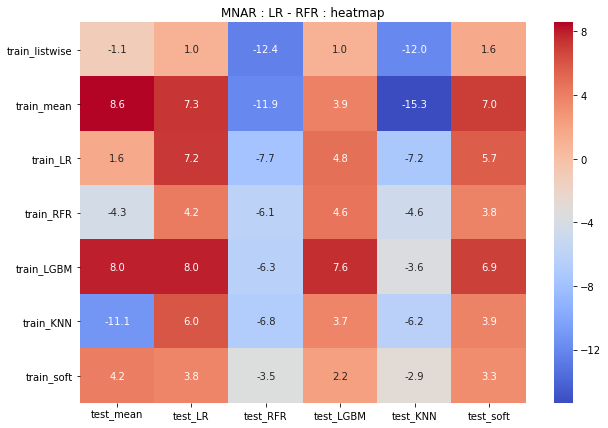
4 考察
今回のシミュレーションにより、様々な欠損補完方法と、その精度検証を行うことができました。
総括としては以下のとおりです。
- 欠損の発生種別により、補完方法、targetの推計方法で大きなばらつきがあり、「これをやれば正解」というモデルは無さそうである
- 禁則とされていた平均値置換も、場合により高い精度を得る可能性がある
また、課題として以下のようなことがあげられます。
- 今回は総500レコードの小規模なデータセットであり、大規模データでも同様の事象になるとは限らない
- 欠損値補完に使用したモデルや、target予測に使用したモデル、いずれもパラメーター調整を行っていない
パラメーター調整を行えば、精度は大きく変化する可能性がある
以上、結論としては、機械学習タスクによる欠損値補完処理は、いくつかのパターンを試行・検証することが最適なのではないかと考えられます。